タイトルが思いつかないので手抜きのタイトルで申し訳ございません。木曜日は小学生の授業はなくて中学3年生だけです。中学3年生は1日約3時間です。これは選択などではなく全員一律です。講習やテスト前でもなく通常時の授業で3時間という塾は結構少ないと思います。うちの塾は規模は小さいですが、なるべく多くの勉強時間を確保したいと考えています。
期末も終わって北辰も終わったのでラストスパートです。まずは教科書で終わりきっていない数学と社会と理科の内容を終わらせます。国語と英語はもう教科書は関係ありません。今日は理科と数学の学習を行いました。
理科は最後の単元の天体です。先に学校で少し習っているようなので説明がやや省略できます。学校が先だろうと塾が先だろうと生徒が理解できればそれでいいのです。ですから私はどうしても学校より先に進もうとか学校には負けないとかそういう意識がほとんどありません。解けるようになればいいのです。天体は地学ということで覚えることの方が多いのですが、それでも若干考える問題もあります。苦手な生徒が多いのが方角です。社会と違って上が北という常識が通用しません。透明半球での方角や北極側から見た方角とか、さらに場所によって違う東西南北を理解しなければなりません。
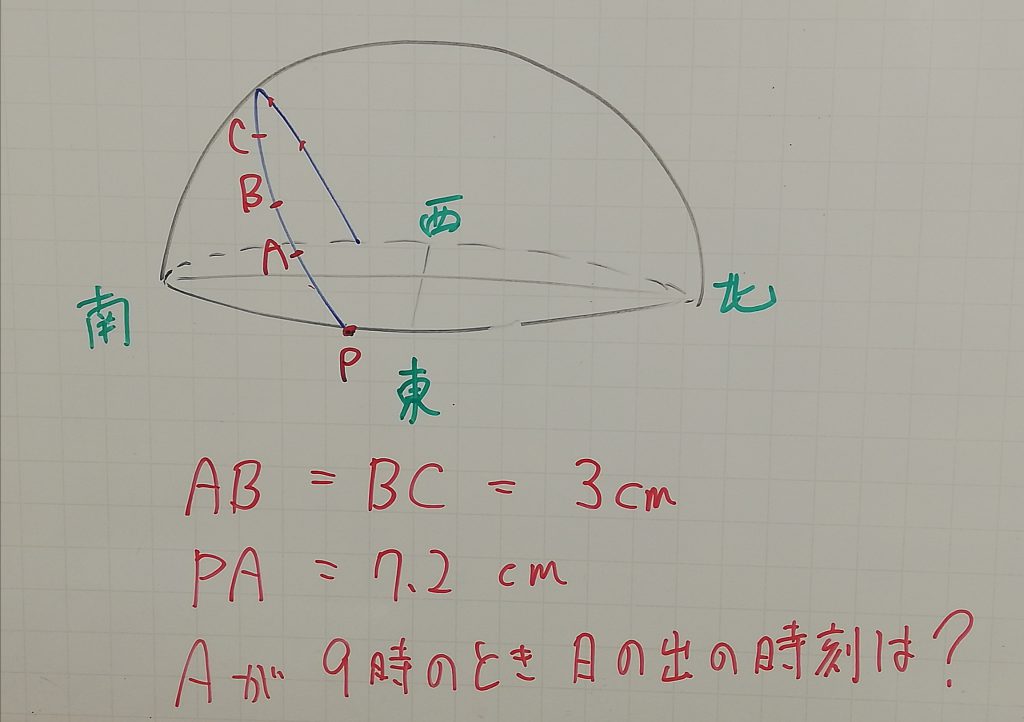
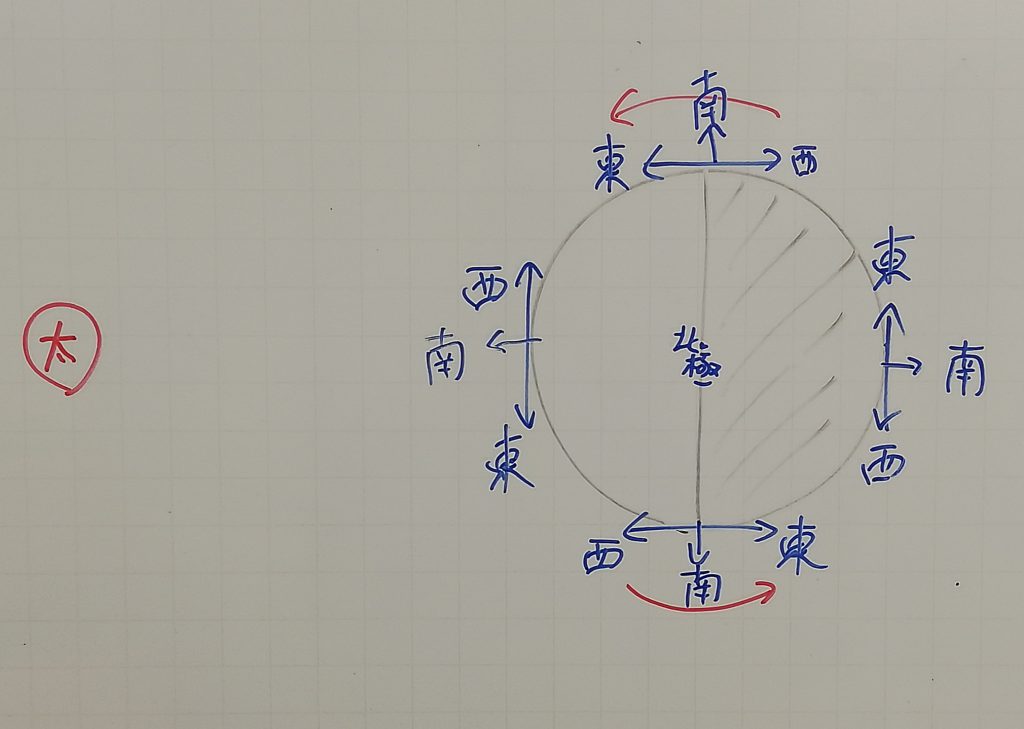
はたして理解してくれたでしょうか。この後問題演習を繰り返しながら定着させたいと思います。
数学は相似からの面積比とか体積比です。一見図形の問題ですが、ほぼ計算問題です。
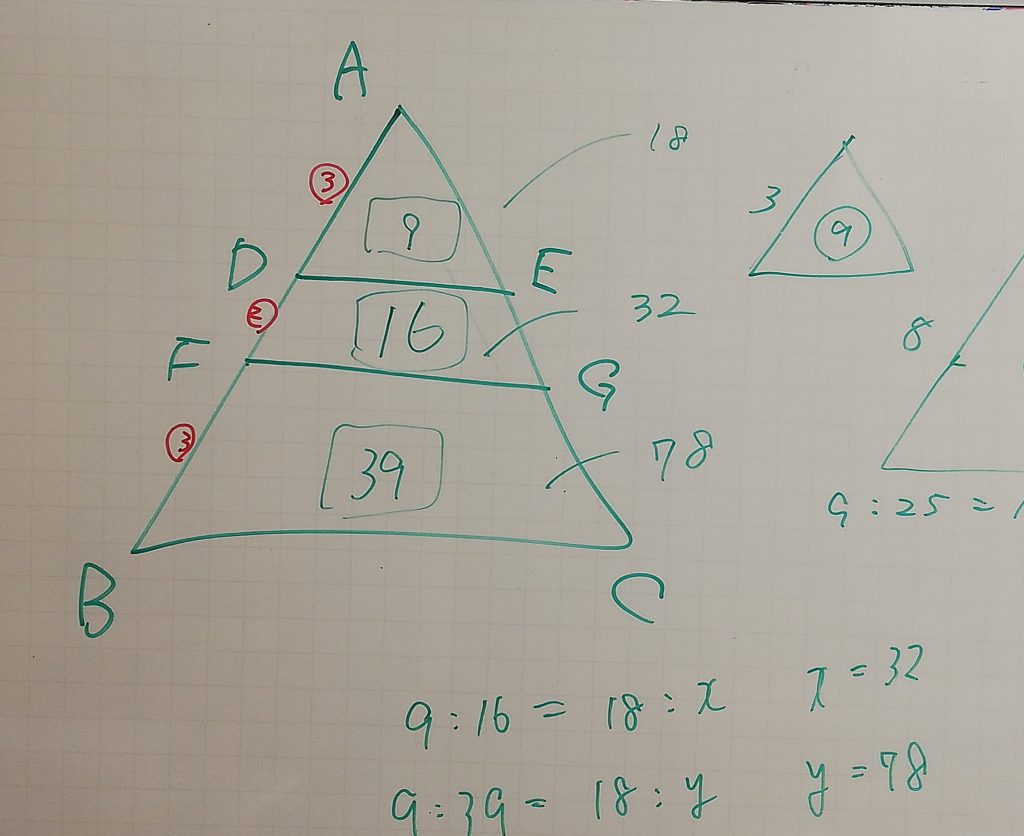
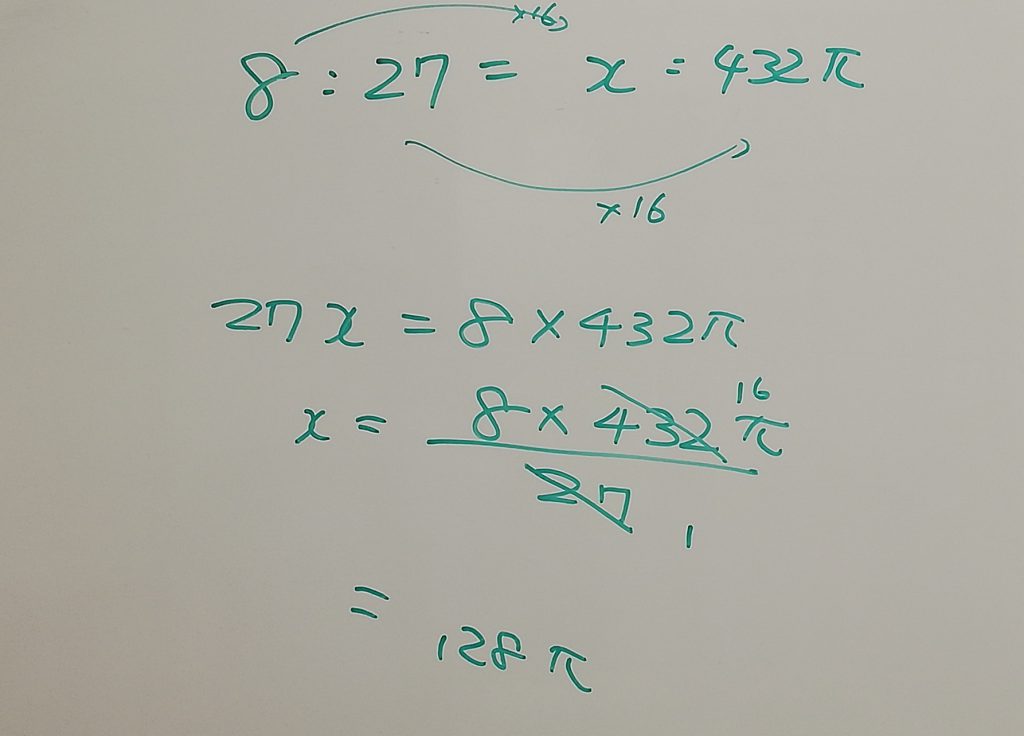
比例式は小学生で出てきて中1でも登場。中1では小学生とは違う解き方を習うため画像のような問題でも、内項の積=外項の積 で解くことに慣れてしまっています。ただその場合でもなるべく簡単に解が求められるような方法を教えました。こういう細かいことは動画とか問題集の解答では分かりません。塾に来ている人だけが知ることのできる解き方というのもあるのです。(それを教えられるかどうかは教える人にもよりますが)
次回は円周角の定理で、最後の最後に残っている大物=三平方の定理は来週入れるでしょうか。前に5年生と6年生の教科書のバランスが悪いと書きましたが、中2と中3にも同じことが言えます。中3は内容が多すぎます。一部中2に移動してもいいくらいです。ちなみに今中3で学習している相似と円周角の定理は以前(といっても相当以前)は中2の内容でした。これが中2に戻ってくれれば中3はもう少し余裕を持てるのですが。
